Work led by Stefan Groha on a new method for multi-state survival analysis is now online on arxiv:

Neural ODEs for Multi-State Survival Analysis.
S Groha, SM Schmon, A Gusev. 2020

When analyzing time-to-event / survival data in a clinical setting we are often interested in understanding the causes of multiple possible and competing outcomes (illness versus death, or response/relapse/death, for example). Existing “multi-state” survival models typically require strong assumptions about the survival trajectory and cannot model a highly complex feature space to build sophisticated predictors. In this work, we propose a new multi-state survival model that leverages recent advances in neural ordinary differential equations to model continuous trajectories without strong assumptions, while being flexible enough to fit complex non-linear interactions between time-dependent predictors. Under the hood, a variational latent variable model allows for estimates of uncertainty as well as time-dependent patient clustering. We show that our method retains the predictive accuracy of cutting edge models while improving calibration and flexibility.

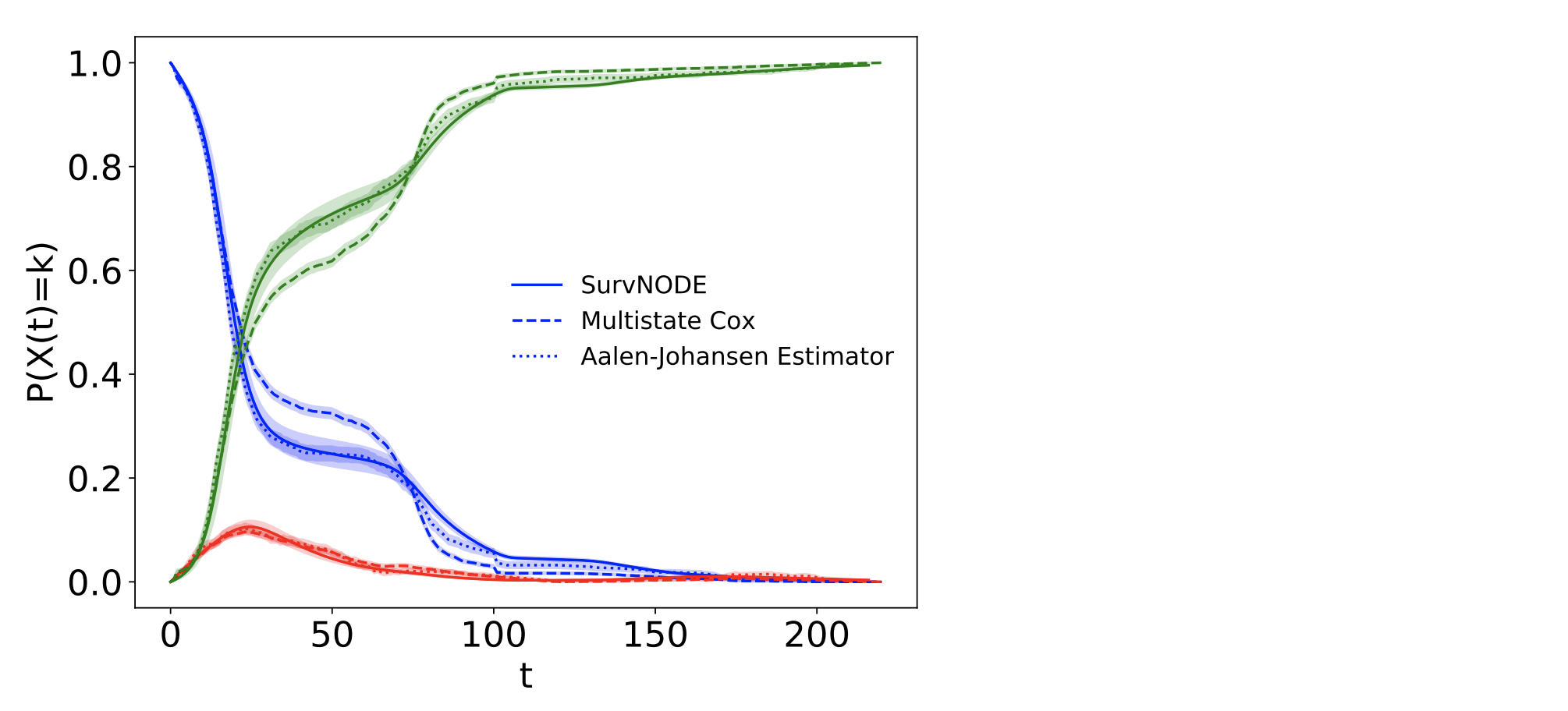
multi state survival

Probability of being in each state over time inferred by the proposed model (solid line)